神经网络概述
神经网络的目标与一个普通的函数相同,即给定输入,期望得到一个处理后的结果,只不过有些时候输入输出间的关系十分复杂,而神经网络可以通过学习的方式得到输入输出之间的关系。
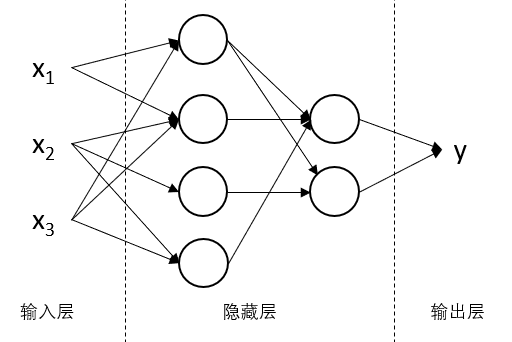
上图即为一个神经网络,分为输入层、隐藏层和输出层,其中隐藏层就是神经网络的关键所在。其中每个圆圈代表一个“神经元”,而箭头则代表这些数据影响着所指的神经元,并一层层最终影响结果。
Logistic 回归
概述
在许多场景下,我们通常只要判断一个东西是或不是,比如判断一张图中是否有人,这种只有两种结果(0 与 1)的称之为 二分分类 。
Logistic 回归是一种用于针对二分分类问题的学习方法,在给定输入 \(x\) 的情况下,输出为真的概率 \(\hat{y}=P(y=1 \vert x)\) ,其中 \(x\) 为 \(n_x\) 维输入向量,\(n_x\) 为特征数量。
为了达到这一目标,引入另一个\(n_x\)维向量\(w\)称为 权重 ,向量中每一个值都是输入的 \(x\) 中对应值的权重。另外还引入一个实数 \(b\) 称为 阈值 。Logistic 回归计算的就是 \(w^T x + b\) ,然而这一函数的问题在于其可以计算出任意值,而 \(y\) 作为一个概率必定落在 \([0,1]\) 中,所以还另引入一个函数 \(\sigma (z) = \frac{1}{1+e^{-z}}\)。
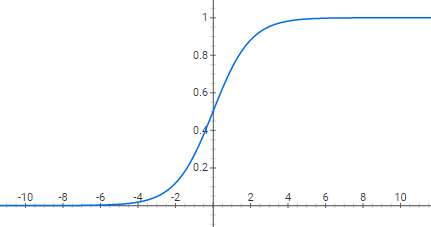
从上图可以看出对于任意值都可以将其映射到 \([0,1]\) 中,且 \(\sigma (0) = 0.5\)。
综上,Logistic 回归通过训练 \(w\) 和 \(b\),然后通过下面这个公式得到结果。
\[\hat{y} = \sigma (w^T x + b)\]成本函数
为了定量表示当前训练出的数据与测试,引入 损失函数 这一概念。
对于给定的测试集 \({(x^{(1)},y^{(1)}),\cdots ,(x^{(m)},y^{(m)})}\),其中 \(x^{(i)}\) 代表第 \(i\) 个数据。显然我们希望计算出的 \(\hat{y}^{(i)}\) 与测试数据 \(y^{(i)}\) 相同,或者说差距尽可能地小。对于 Logistic 回归,损失函数可以为
\[L( \hat{y}^{(i)}, y^{(i)}) = -(y^{(i)}log(\hat{y}^{(i)})) + (1- y^{(i)})log(1-\hat{y}^{(i)})\]由于 \(y\) 取值只有 0 与 1 ,所以只有如下两种情况
- 当 \(y = 0\) 时,\(L( \hat{y}^{(i)}, y^{(i)}) = log(1-\hat{y}^{(i)})\),此时 \(\hat{y}\) 越接近 \(0\), \(L\) 越小。
- 当 \(y = 1\) 时,\(L( \hat{y}^{(i)}, y^{(i)}) = -log(\hat{y}^{(i)})\),此时 \(\hat{y}\) 越接近 \(1\), \(L\) 越小。
损失函数并不唯一,但在这里用该函数作为损失函数可以使得其只有一个最小值,所以只有一个全局最优解,而非多个局部最优解,使得寻找最优解更为方便。
损失函数作用于一组数据,为了能够描述整个数据集引入 成本函数
\[J(w,b) = \frac{1}{m} \sum_{i=1}^m L( \hat{y}^{(i)}, y^{(i)})\]即所有数据损失函数结果的平均值。我们的目标就是找到使得成本函数最小的那一组 \((w,b)\) 。
梯度下降法
下图为损失函数与权重之间的关系,我们目标是找到成本函数最低时候那个权重。
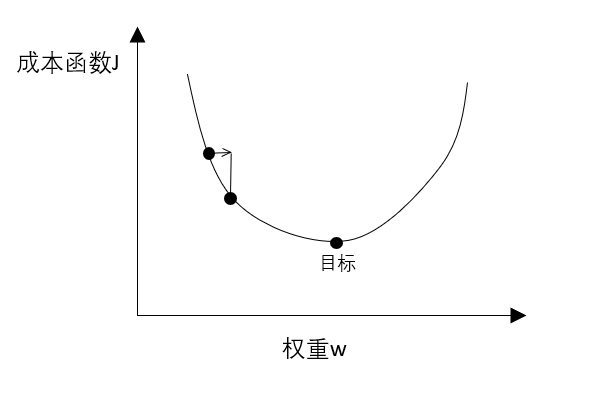
根据微积分的知识,沿着切线方向下降最快,因此有
\[w = w - \alpha \frac{dJ(w)}{dw}\]其中 \(\alpha\) 称之为 学习速率。通过这一式子,无论当前点在目标左侧还是右侧,导数正负都能控制其往目标点移动。而且当离目标点较远时倒数较大,所以每次移动较多,越接近时导数越小,移动的也较小。
这是二维的一个例子,对于更多维的将其中导数换为相应变量的偏导数即可,如 Logistic 回归中有
\[w = w - \alpha \frac{\partial{J(w)}}{\partial{w}} , b = b - \alpha \frac{\partial{J(b)}}{\partial{b}}\]计算图
前向传播
考虑 \(J = 3(a + bc)\) 这一式子,可以根据计算顺序得到下面这幅图
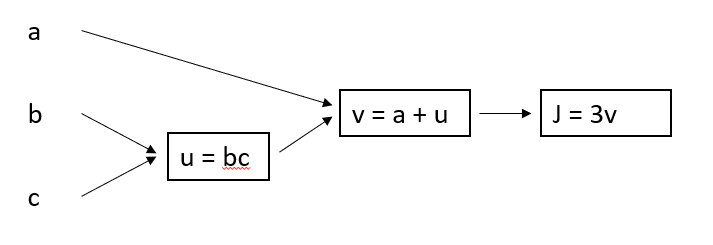
给定输入后,从左往右便可以计算出 \(J\),这样的计算方式称之为 正向传播。
反向传播
反向传播同样用的是这幅图,只是方向从右往左,希望找到的是 \(J\) 变化的时候其他的变量是如何影响它的。
简单的说就是计算导数,想要找到 \(v\) 如何影响 \(J\),只需要计算 \(\frac{dJ}{dv}\) ,这样的一步称为反向步。
当想要找到 \(a\) 如何影响 \(J\),可以先计算 \(a\) 如何影响 \(v\),\(v\) 如何影响 \(J\),即 \(\frac{dJ}{da} = \frac{dJ}{dv} \frac{dv}{da}\),其实就是微积分中的链式法则。整个学习过程中,首先通过正向传播得到结果,与期望值不符则再用反向传播利用梯度下降反过来影响输入,不断反复达到学习的效果。
Logistic 回归中的应用
总结下 Logisitc 回归中的过程,有如下几个式子
- \[z = w^T x + b\]
- \[\hat{y} = a = \sigma (z)\]
- \[L(a,y) = -(ylog(a)+(1-y)log(1-a))\]
从而可以得到如下的计算图。
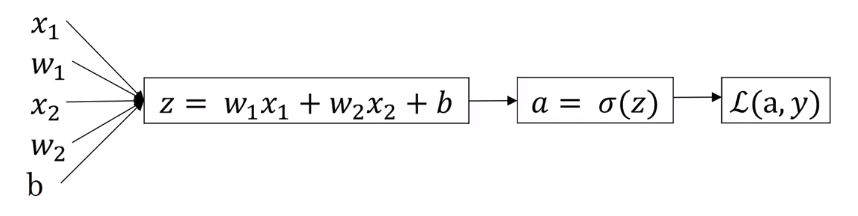
在给定输入的时候能计算出 \(J\),而我们的目标是找到 \((w1,w2,b)\) 如何取值可以使得 \(J\) 最小。
为了找到 \(w1\) 如何影响 \(J\) ,需要运用反向传播。通过求导可以计算出
\[\frac{dL}{da}= - \frac{y}{a} + \frac{1-y}{1-a}\\ \frac{dL}{dz} = \frac{dL}{da} \frac{da}{dz} = a-y\]又有 \(\frac{\partial{L}}{\partial{w_1}} = x_1 \frac{dL}{dz}\) ,所以梯度下降每次迭代 \(w_1 = w_1 - \alpha dw_1\) ,\(w_2, b\) 同理。
综上,可以得到 Logistic 回归的代码。
1
2
3
4
5
6
7
8
9
10
11
12
J = dw1 = dw2 = db = 0
for i = 1 to m
// 正向传播
z[i] = w^T * x[i] + b
a[i] = sigma(z[i])
J += L(a,y)
// 反向传播
dz[i] = a[i] - y[i]
dw1 += x1[i] * dz[i]
dw2 += x2[i] * dz[i]
db += dz[i]
J /= m, dw1 /= m, dw2 /= m, db /= m
向量化
向量化简而言之就是将我们之前所用到的各种 \(w_1, x_1\) 之类的放到一个向量中,这样子计算的时候可以用 numpy 中各种并行算法加速运行,例如
\[X = \begin{bmatrix} x^{(1)} \cdots x^{(m)} \end{bmatrix}, Y = [y^{(1)},\cdots,y^{(m)}]\\ dz = [dz^{(1)}, dz^{(2)}, \cdots , dz^{(m)}]\\ w = \begin{bmatrix} w_1\\ \vdots\\ w_n \end{bmatrix}\]其中对于 \(X\) 中每个向量以列的方式存储。所以 Logistic 回归可以进一步优化为
1
2
3
4
5
6
7
8
z = np.dots(w.t, x) + b
a = sigma(z)
dz = a - y
dw = np.dots(x, dz.t) / m
db = np.sum(dz) / m
w = w - alpha * dw
b = b - alpha * db
这样就可以完成一次高效的学习,之后只需要不断重复这一过程就可以完成 Logistic 回归。